알고리즘 성능 평가

알고리즘 성능 평가를 위해서는 '복잡도(Complexity)의 척도'를 사용한다
동일한 기능을 수행하는 알고리즘이 있을 때, 복잡도가 낮을수록 좋은 알고리즘이다

복잡도

복잡도에는 시간 복잡도와 공간 복잡도가 있다

시간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 수행 시간 분석
공간 복잡도 : 특정한 크기의 입력에 대하여 알고리즘의 메모리 사용량 분석

서로 다른 알고리즘을 비교할 때는 동일한 하드웨어 환경에서, 사용하는 소프트웨어의 환경도 고려해야 한다.
예를 들어 C언어와 같은 컴파일 언어의 경우 인터프리터 언어에 비해 실행 속도가 빠르다

시간 복잡도(Time Complexity)

특정 알고리즘이 어떤 문제를 해결하는 데 걸리는 시간을 의미
같은 결과를 갖는 코드라면 시간이 적게 걸릴수록 좋은 코드이다

시간 복잡도는 절대적 실행 시간이 아니라, 알고리즘을 수행하는 데 연산이 몇 번 이루어지는지를 숫자로 표기한다

빅오(Big-O) 표기법

빅오 표기법은 최악의 경우(worst case)를 계산하는 방식이다
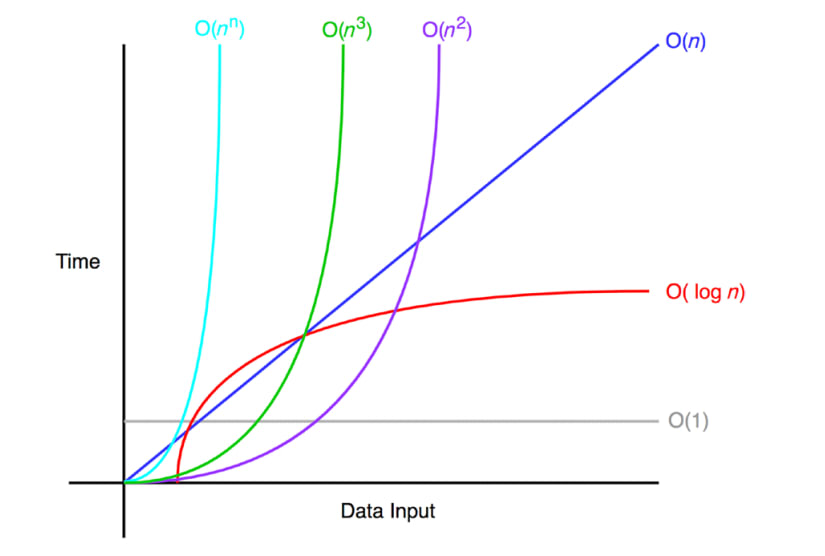
Pasted image 20240712003620.jpgPasted image 20240711234521.png
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(2^n) 순으로 오른쪽으로 갈수록 효율이 떨어진다

N의 크기에 따른 시간 복잡도를 대략적으로 나타내면 아래와 같다
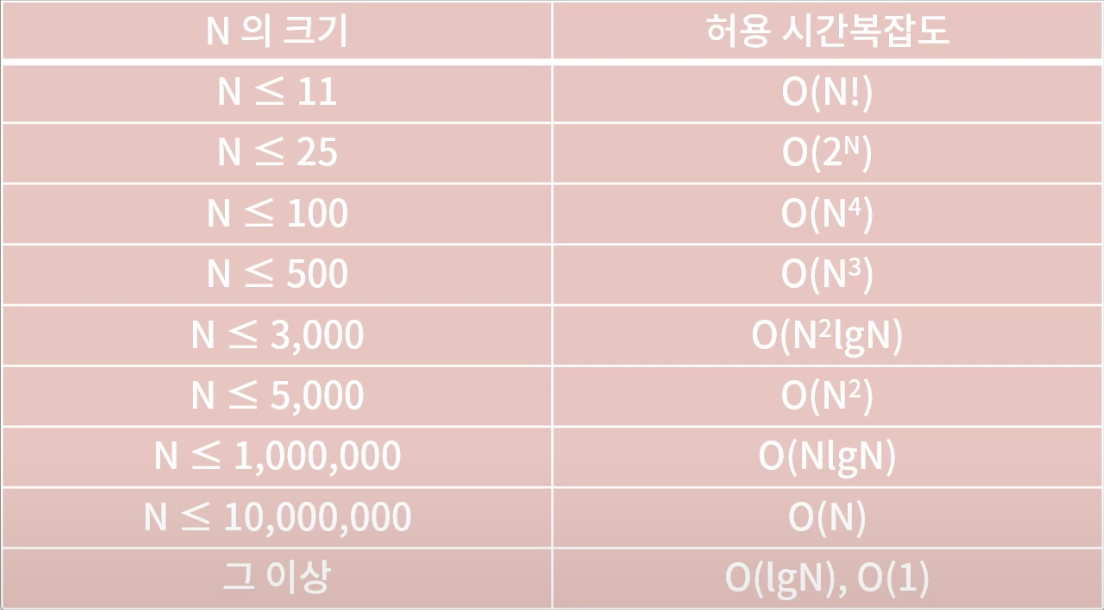
Pasted image 20240711234600.png
N^2 은 5000 정도까지만 허용된다고 생각하자
로그는 거의 밑이 2이기 때문에 계산 시 log 1000은 10, log 2000은 11, log1000000(1백만) 은 20이라고 보면 된다

빅오 표기법의 특징

  1. 상수항 무시
    빅오 표기법은 n이 충분히 크다고 가정하기 때문에 O(2n) -> O(n)으로 간주한다

  2. 영향력 없는 항 무시
    빅오 표기법은 n의 크기에 영향을 받으므로 가장 영향력이 큰 항 이외에 영향력이 없는 항은 무시한다. O(n^2 + 2n + 1) -> O(n^2)으로 간주한다

시간 복잡도 줄이는 방법

시간 복잡도에서는 반복문이 가장 시간 소모에 큰 영향을 미친다
따라서 반복문의 숫자를 줄일수록 시간 복잡도를 줄일 수 있다

자료 구조와 알고리즘을 적절히 사용해서 시간 복잡도를 줄일 수도 있다

대표적인 시간복잡도 예시
복잡도 소요 시간 예시
O(1) 상수 시간 스택에서 Push, Pop
O(log n) 로그 시간 이진 트리
O(n) 직선적 시간 for 문
O(n log n) 선형 로그 시간 퀵 정렬(quick sort), 병합 정렬(merge sort), 힙 정렬(heap sort)
O(n^2) 2차 시간 이중 for 문, 삽입 정렬(insertion sort), 거품 정렬(bubble sort), 선택 정렬(selection sort)
O(C^n) 지수 시간 피보나치 수열
BFS, DFS : O(V+E)
시간 복잡도를 구하는 요령

  • 하나의 루프를 사용하여 단일 요소 집합을 반복하는 경우: O(n)- 컬렉션의 절반 이상을 반복하는 경우: O(n / 2) -> O(n)
  • 두 개의 다른 루프를 사용하여 두 개의 개별 콜렉션을 반복하는 경우: O(n + m) -> O(n)
  • 두 개의 중첩 루프를 사용하여 단일 컬렉션을 반복하는 경우: O(n²)
  • 두 개의 중첩 루프를 사용하여 두 개의 다른 콜렉션을 반복하는 경우: O(n * m) -> O(n²)
  • 컬렉션 정렬을 사용하는 경우: O(n*log(n))

자료구조별 시간 복잡도

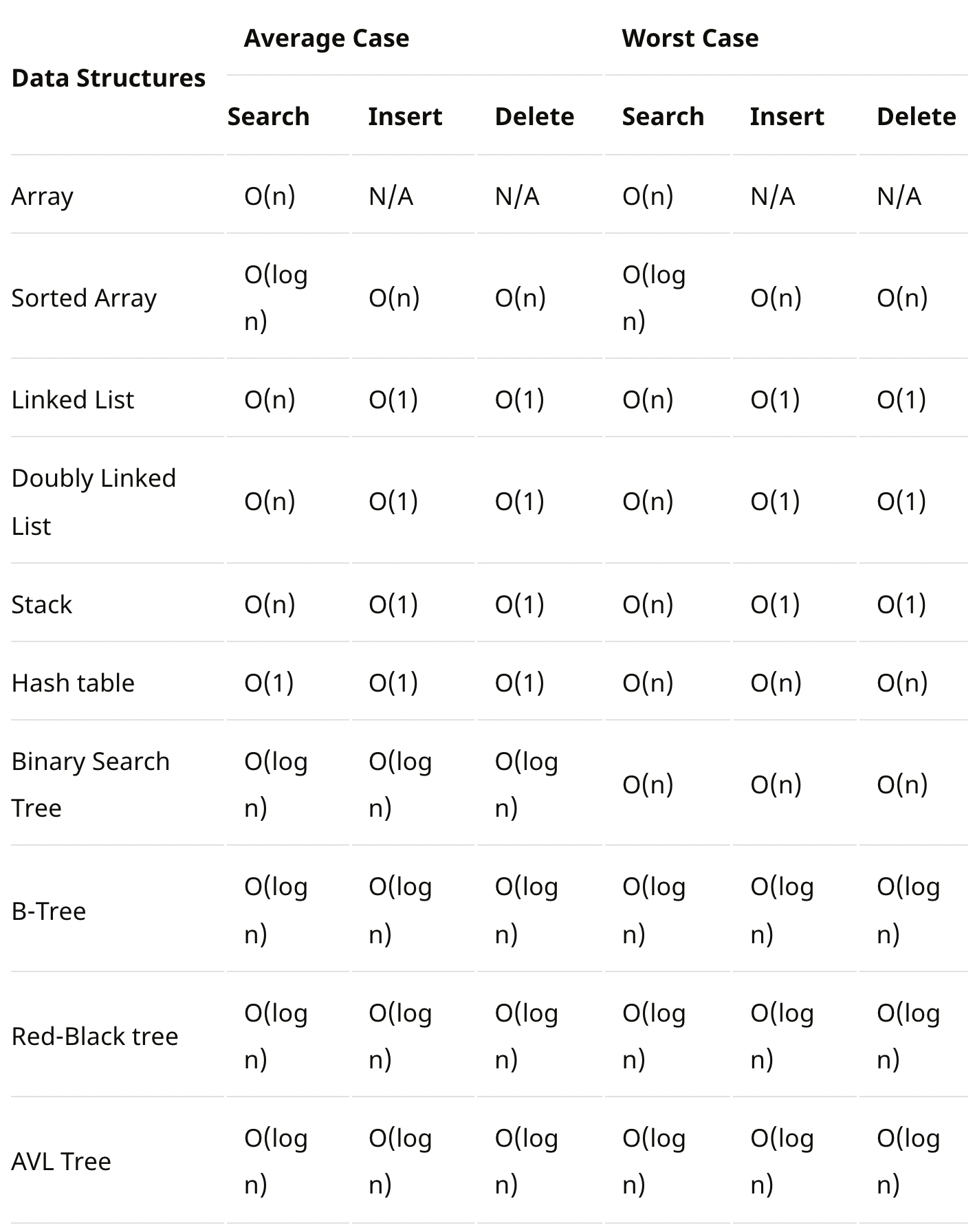
Pasted image 20240712004242.png

알고리즘별 시간 복잡도

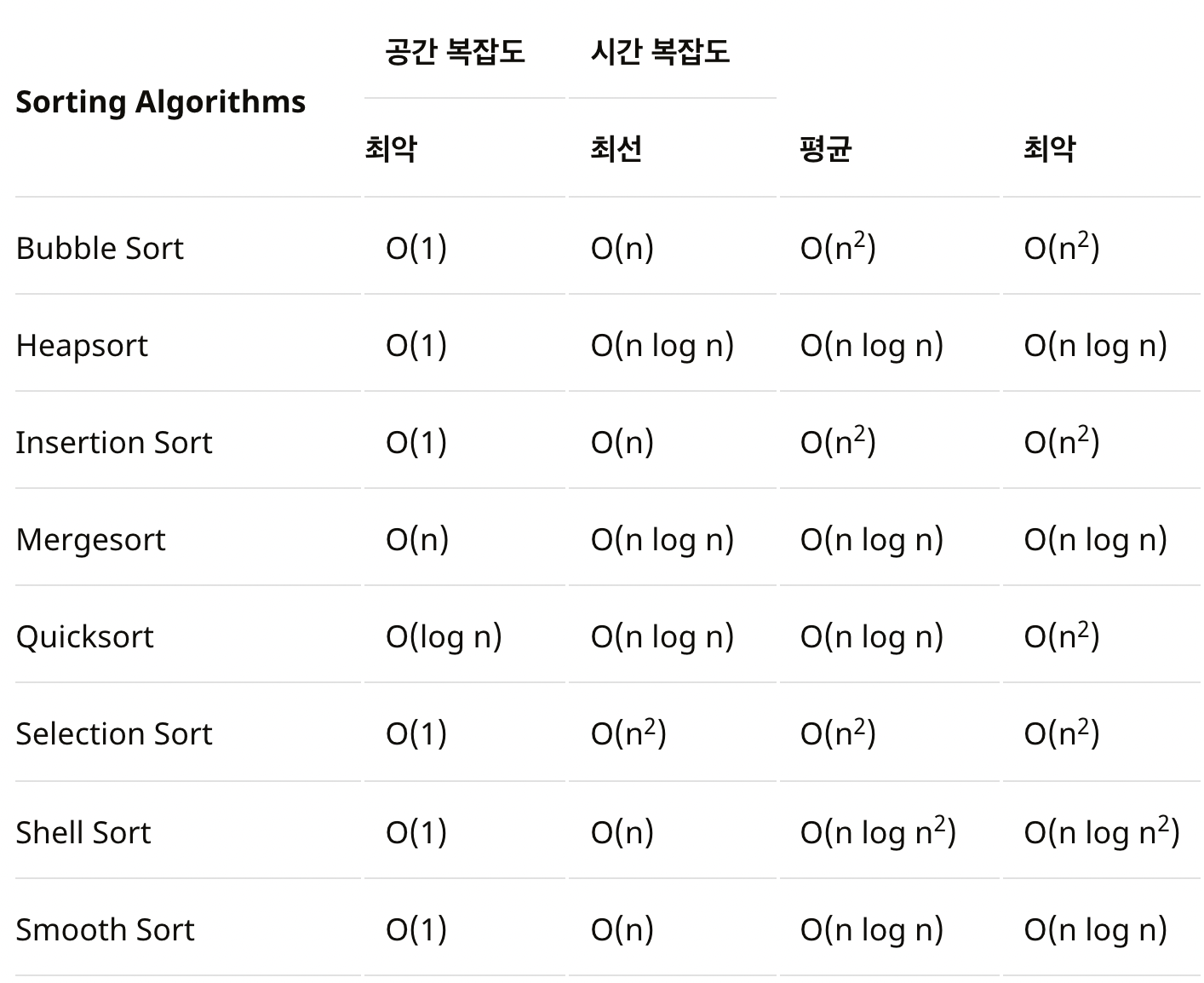
Pasted image 20240712004304.png

실행 시간 예측(1초 기준)
O(1), O(log N) N    <=    ∞
O(N) N    <=    100,000,000(1억)
O(N log N) N    <=    13,993,959(1천 3백만)
O(N²) N    <=    10,000(1만)
O(N³) N    <=    464
O(2ᴺ) N    <=    26
O(N!) N    <=    12

컴퓨터가 1억~2억 번의 연산을 하기 위해서는 약 1초의 시간이 필요하다

공간 복잡도(Space Complexity)

작성한 프로그램이 얼마나 많은 메모리를 차지하는지 분석하는 방법
보통 메모리 사용량 기준은 MB 단위로 제시되며, RAM 사용량과 관련이 있다

공간 복잡도에는 '고정 공간' 과 '가변 공간' 이 있는데, 공간 복잡도는 이 둘의 합이다

고정 공간

입출력과 관계 없는 공간
단순 변수, 상수 변수와 같이 고정적으로 정의된 변수

가변 공간

동적인 공간
특정 인스턴스에 의존하는 크기를 가진 구조화 변수들이 해당된다
함수 선언에 사용된 인자들, 반복문을 위한 가상의 변수(i 또는 n)이 차지하는 공간

메모리 제한

N짜리 2차원 배열은 O(N^2)
배열이 없다면 O(N) 이라고 보면 된다

일반적으로 메모리 영역에서 데이터 영역이 스택 영역보다 더 크기 때문에 큰 배열은 전역 변수에 선언을 한다.