프림 알고리즘(Prim's Algorithm)
최소 스패닝 트리(MST)를 구하는 알고리즘으로, 하나의 시작 정점을 기준으로 가장 작은 간선과 연결된 정점을 선택하여 신장트리가 될 때까지 모든 노드를 연결시킨다.
이미 만들어진 트리에 인접한 간선만을 고려한다는 점을 제외하면 크루스칼 알고리즘(Kruskal Algorithm)과 완전히 똑같다. 그리디(Greedy) 알고리즘을 바탕에 두는 것도 같다. 즉, 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택한다.
간선의 개수가 적은 경우 크루스칼이 더 용이하지만 대부분의 경우 정점 위주 탐색인 프림이 더 용이하다. 둘 다 시간복잡도는 O(ElogV)로 같다.
동작 과정
- 임의의 정점을 선택한다.
- 선택한 정점으로부터 아직 방문하지 않은 정점까지의 간선을 추가한다. Priority Queue로 구현하면 간편하다.
- 비용의 오름차순으로 정렬된 정점과 이어진 미방문 정점을 탐색한다.
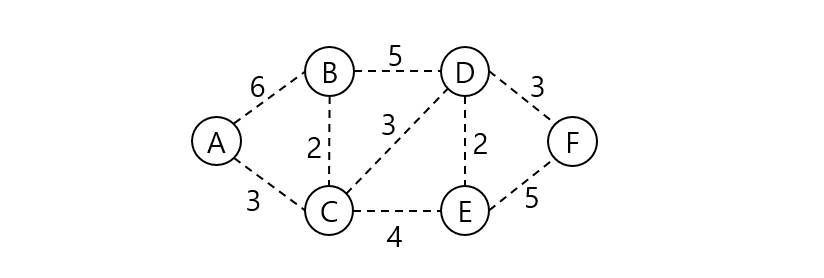
위 그래프의 최소 신장 트리를 프림 알고리즘으로 구해보자. 시작 정점은 A라 한다.
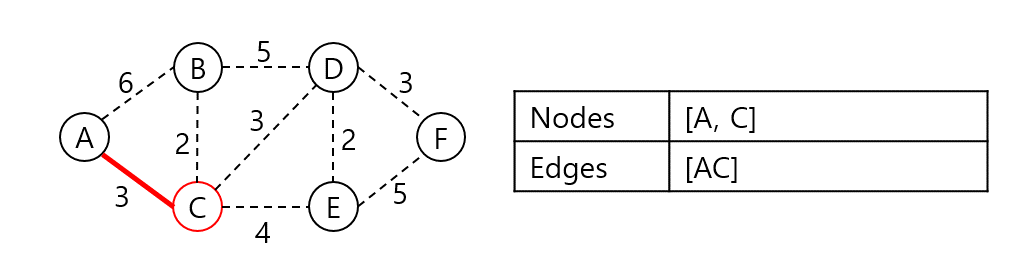
A와 인접한 노드 B, C 중 C가 가장 가중치가 낮은 간선으로 연결되어 있으니 C를 집합에 넣고 비용에 AC 가중치를 더한다.
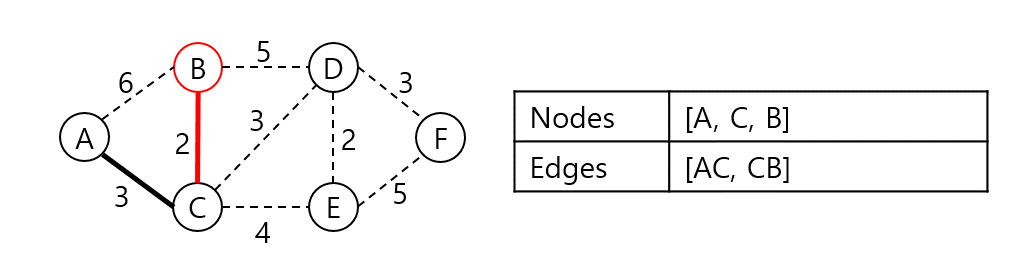
AC와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 B다. 집합에 B를 넣고 CB 가중치를 더한다.
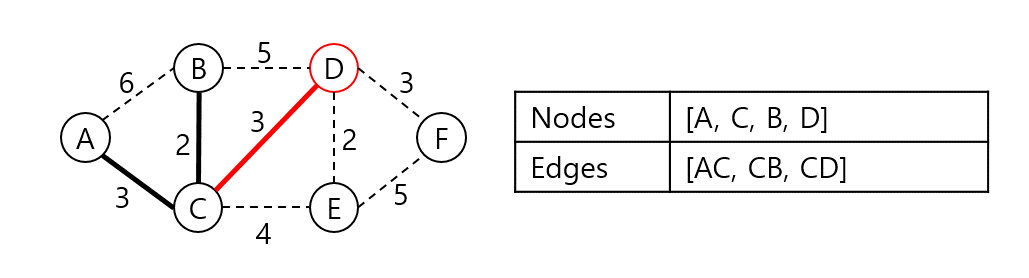
A, C, B와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 D다. 집합에 D를 넣고 CD 가중치를 더한다.
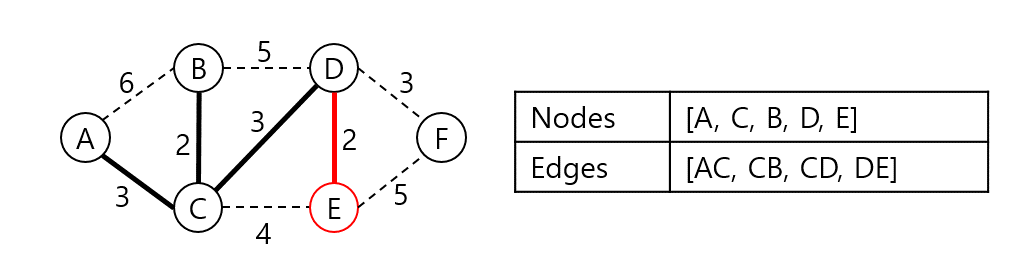
A, C, B, D와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 E다. 집합에 E를 넣고 DE 가중치를 더한다.
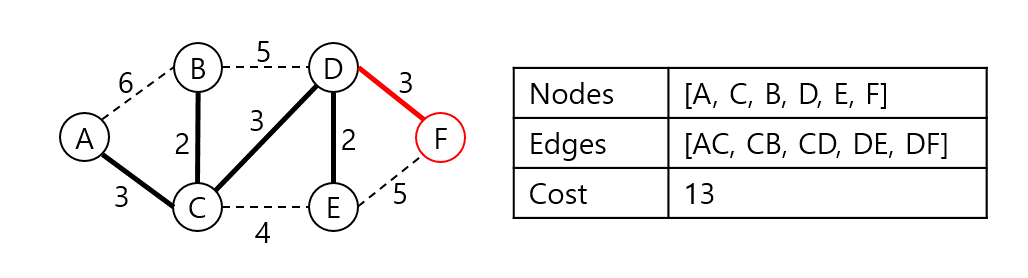
A, C, B, D, E와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점 F를 집합에 넣고 DF 가중치를 더한다. 트리의 집합에 속한 원소의 개수가 N이 되었으므로 탐색을 중단한다. 탐색 결과 최소 신장 트리 구축의 비용은 13으로 확인되었다.
구현
class Node implements Comparable<Node>{
int to;
int value;
public Node(int to, int value) {
this.to = to;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value - o.value;
}
}
public class Main {
static int total;
static List<Node>[] list;
static boolean[] visited;
public static void main(String[] args){
int v = 7;
int[][] graph = {{1,2,29}, {1,5,75},{2,3,35},{2,6,34}, {3,4,7},{4,6,23},
{4,7,13}, {5,6,53}, {6,7,25}};
list = new ArrayList[v+1];
visited = new boolean[v+1];
for(int i=1; i<v+1; i++) {
list[i] = new ArrayList<>();
}
for(int i=0; i<graph.length; i++) {
int a = graph[i][0];
int b = graph[i][1];
int w = graph[i][2];
list[a].add(new Node(b,w));
list[b].add(new Node(a,w));
}
prim(1);
System.out.println(total);
}
static void prim(int start) {
Queue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start,0));
while(!pq.isEmpty()) {
Node p = pq.poll();
int node = p.to;
int weight = p.value;
if(visited[node]) continue;
// 선택한 간선의 정점으로부터 가장 낮은 가중치 갖는 정점 선택
visited[node]= true;
total += weight;
for(Node next : list[node]) {
if(!visited[next.to]) {
pq.add(next);
}
}
}
}
}
시간복잡도
O(Elog V)