Closest Pair

N개의 점들 중 가장 가까운 쌍을 찾는 알고리즘
가까운 쌍 찾기에 대한 접근
-
브루트 포스로 n개의 점에서 나머지 n-1개의 점을 비교한다
1차원 좌표에서 두 점의 거리를 구하기 위해서는 정렬 후 앞에서부터 인접한 점과 비교해가며 탐색하면 되지만,
2차원 좌표에서 두 점의 거리를 구하기 위해서는 한 점에 대해 다른 모든 점을 탐색하기 때문에 O(n^2)이 걸리게 된다 -
분할 정복(Divide and Conquer) 을 사용한다
n개의 점을 x축 기준으로 정렬한 후, x의 중앙값인 점을 찾아 왼쪽과 오른쪽 점들로 문제를 나누어 최소 거리를 찾은 후, 중앙에 걸쳐있는 점을 검사한다.
Closest Pair 아이디어
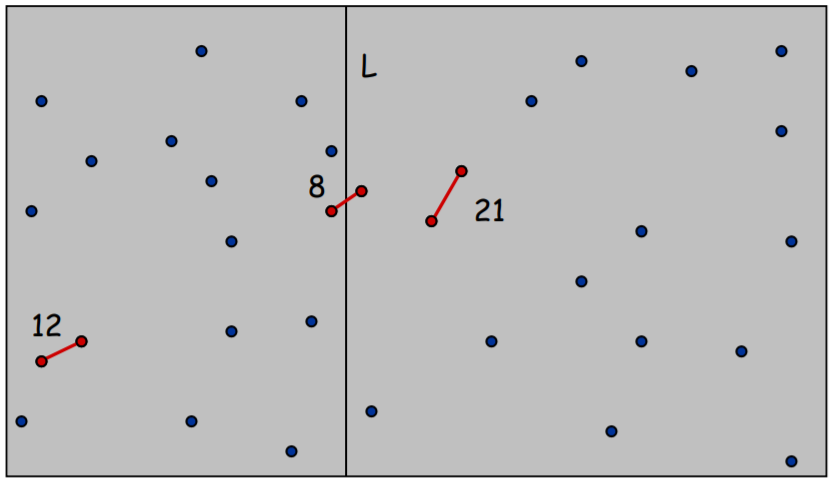
- 양쪽 점의 개수가 n / 2 가 되도록 세로선을 긋는다(분할) - 수행 시간 O(1)
- 각 영역에서 가장 가까운 두 점을 찾는다(정복)
- 각 영역의 closest pair와 두 영역 사이에 있는 closest pair 중 거리가 짧은 것을 반환한다(통합)
통합 과정
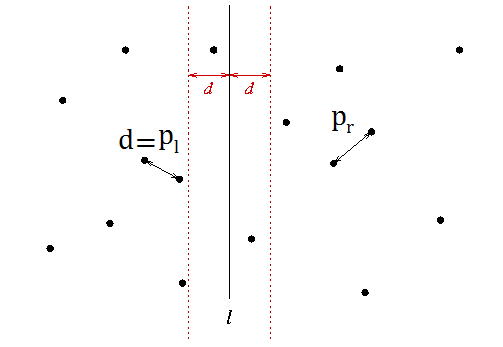
양쪽 영역에서 구한 가장 짧은 거리를 d라고 할 때,
세로선을 중심으로 d만큼 떨어진 영역, 즉 2d 안에서만 조사한다(이 영역을 Band라고 힌다)
그 이상은 살펴볼 필요가 없기 때문이다
그러나, 이 방법을 쓰더라도 대부분이 밴드 영역 안에 있다면 최악의 경우 O(N^2) 가 나올 수 있다
그렇기 때문에 한 가지 아이디어가 더 필요하다.
한 점(p)에서 최대 6개 비교
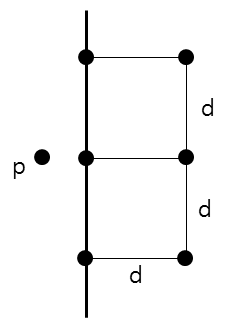
이 예시에서 d는 ==min(왼쪽 영역 최솟값, 오른쪽 영역 최솟값)==이며, 왼쪽 점인 p에서 오른쪽 점과의 거리를 구하려고 한다
이때 p가 검사할 점은 최대 6개이다.
왜냐하면 d x 2d 크기의 직사각형에 들어가 있는 점만 탐색하면 되기 때문이다.
점과 점 사이의 거리가 d보다 작다는 것은 d가 최솟값이라는 것에 모순되므로 점과 점 사이는 d보다 같거나 커야 한다. 그리고 최악의 경우 위와 같은 배치로 p에서는 6개의 점을 탐색하게 될 것이다.
격자를 움직이자
위에서 d x 2d 크기의 격자를 옮겨가며 d보다 작은 최솟값이 나오는지 검사하면 된다.
따라서 Band 영역 안에 있는 점들을 y좌표를 기준으로 정렬시킨 후, 순차적으로 격자 크기 만큼만 탐색하면 된다.
그 결과 밴드 안에 있는 y좌표로 정렬하는 시간 O(nlogn)이 소요 되고, 분할 정복에서도 각 O(n)을 log n번 수행하므로 시간복잡도는 O(n (log n)^2) 이 된다.
Merge 최적화
그러나 분할 정복을 이용하는 알고리즘인 만큼, 병합 정렬(Merge sort)를 활용해서 이를 ==O(nlog n)==으로 줄일 수 있는 아이디어가 있다.
합쳐진 상태에서 y좌표로 정렬하는 것이 아니라, 작게 분할된 상태에서 y좌표로 정렬하며 merge 한다면 정렬 시간이 O(n) 이 걸리게 된다.
이를 통해 y좌표로 정렬하는 시간이 O(nlog n)에서 O(n)으로 바뀌면서 O(n(log n)^2) 에서 O(nlog n) 시간복잡도가 된다
| 항목 | 최적화 전 O(n (log n)²) | 최적화 후 O(n log n) |
|
|
|
|
| 초기 정렬 | O(n log n) | O(n log n) |
| 재귀 분할 | T(n) = 2T(n/2) + C(n) | T(n) = 2T(n/2) + C(n) |
| 결합 단계 (C(n)) | O(n log n) | O(n) |
| - 중간 띠 선별 | O(n) | O(n) |
| - y 좌표 정렬 | O(n log n) (매번 새로 정렬) | O(n) (정렬 상태 유지) |
| - 거리 비교 | O(n) | O(n) |
| 재귀 관계식 | T(n) = 2T(n/2) + O(n log n) | T(n) = 2T(n/2) + O(n) |
| 각 레벨 비용 | O(n log n) | O(n) |
| 트리 높이 | log n | log n |
| 총 시간 복잡도 | O(n (log n)²) | O(n log n) |
\
왜 원형 영역이 아닐까?
이 알고리즘을 공부하면서 가장 궁금했던 건, 왜 격자 모양으로 탐색할까? 였다
한 점에서 d보다 작은 영역을 탐색하기 위해선 길이 δ의 원형 영역을 보는 것이 정확하다고 생각했기 때문이다.
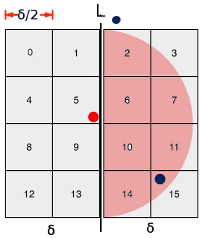
위의 그림은 한 면이 δ / 2 이기 때문에 8개를 이어붙인 것이 δ x 2δ 와 같다고 보면 된다
이렇듯 앞서 최대 6개의 점을 검사한다고 했지만, δ x 2δ 크기의 격자 안에는 p가 검사를 해야 하는 점까지 d보다 떨어져있는 영역이 포함되어 있기 떄문에 6개까지 검사할 필요가 없다
나름 찾아본 결과 다음과 같은 근거들이 있었다.
계산의 단순성
원형 영역을 사용하면 매 비교마다 (x1-x2)² + (y1-y2)² < δ² 계산을 해야하는 반면, 정사각형은 |x1 - x2| < δ , |y1 - y2| < δ 로 쉽게 체크할 수 있다
원은 제곱근 계산을 매번 해야하는 것에 반해, 사각형은 단순 뺄셈, 덧셈으로 가능하다
또한, 2차원 평면을 격자로 나눴을 때 분할 정복 접근법과도 잘 맞고, 알고리즘을 분석하기도 더 쉽다
충분한 커버리지
사각형이 원을 포함하므로, 모든 가능한 가까운 점들을 확실하게 포함하게 된다.
약간의 추가 영역을 검사하지만, 알고리즘의 정확성에는 문제가 없다
차원 확장의 용이성
3차원 이상의 공간으로 알고리즘을 확장할 때도 정육면체 형태로 쉽게 확장할 수 있다
결론적으로, 정사각형 영역을 사용하는 것은 추가 영역을 조금 더 검사하는 대신 전체적인 알고리즘의 성능과 이해도를 높이는 트레이드오프라고 할 수 있겠다.