병합 정렬(Merge sort)

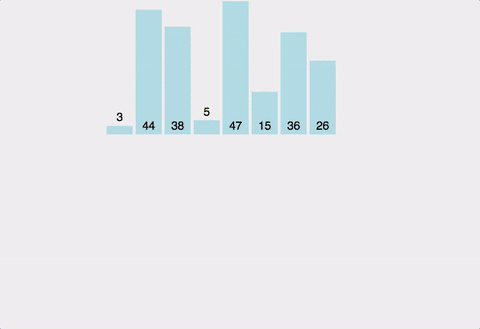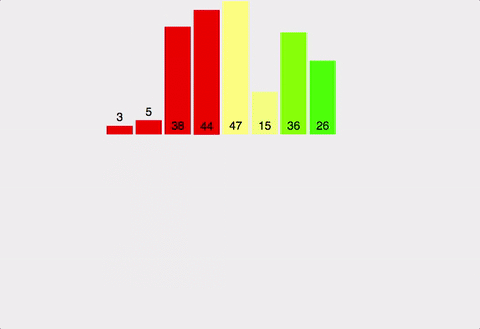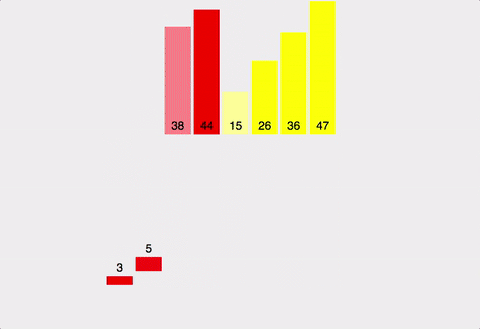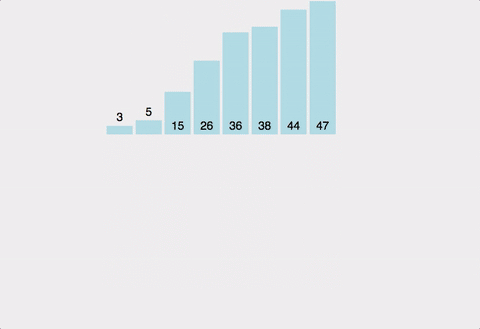
분할 정복(Divide and Conquer)방식을 사용해 배열을 반으로 나눈 후, 각 부분을 재귀적으로 정렬하고 마지막에 병합하는 방식의 정렬 알고리즘

완전 이진 트리를 사용한다

시간복잡도

최선도, 평균도, 최악의 경우도 O(NlogN)
데이터를 정확히 반으로 나눠 정렬하므로 일정한 시간 복잡도가 유지된다

LinkedList 정렬

병합 정렬은 순차적인 비교로 정렬을 진행하므로, LinkedList 정렬이 필요할 때 사용하면 효율적이다
LinkedList는 순차적 접근은 효율적이지만, 임의 접근은 비효율적이기 때문이다.

강점

1. 노드의 연결만 변경하면 되므로, 추가 메모리 사용을 최소화 할 수 있다
2. 정렬된 두 개의 LinkedList를 병합하는 것은 포인터만 조작하면 되므로 효율적이다

다른 정렬 알고리즘과의 비교:

• 퀵 정렬: 임의 접근이 필요하므로 LinkedList에 비효율적
• 힙 정렬: 역시 임의 접근이 필요해 LinkedList에 적합하지 않음
• 삽입 정렬: LinkedList에 적용 가능하지만, 대규모 데이터에 대해 병합 정렬보다 비효율적

퀵 정렬(Quick Sort)과의 차이

퀵 정렬 : 우선 피벗을 통해 정렬(partition) 후 영역을 쪼갠다(QuickSort)
병합 정렬 : 영역을 쪼갤 수 있을 만큼 쪼갠(MergeSort) 후 정렬(merge)한다

코드

public class MergeSorter {

    public static void mergeSort(int[] arr) {
        sort(arr, 0, arr.length);
    }

    private static void sort(int[] arr, int low, int high) {
        if (high - low < 2) {
            return;
        }

        int mid = (low + high) / 2;
        sort(arr, 0, mid);
        sort(arr, mid, high);
        merge(arr, low, mid, high);
    }

    private static void merge(int[] arr, int low, int mid, int high) {
        int[] temp = new int[high - low];
        int t = 0, l = low, h = mid;

        while (l < mid && h < high) {
            if (arr[l] < arr[h]) {
                temp[t++] = arr[l++];
            } else {
                temp[t++] = arr[h++];
            }
        }

        while (l < mid) {
            temp[t++] = arr[l++];
        }

        while (h < high) {
            temp[t++] = arr[h++];
        }

        for (int i = low; i < high; i++) {
            arr[i] = temp[i - low];
        }
    }
}